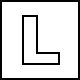This is part 1 of a paper I wrote for Ken Forbus’ Qualitative Reasoning course, adapted for this blog. You can find a printable version of the paper here and part 2 here.

Computers that play chess, otherwise known as chess engines, have existed since at least the late 1940s. Because the game was said to require the perfect combination of planning, strategy, psychology, and calculation, chess was once thought to be an activity directly correlated with intelligence, and that only a truly intelligent computer should be able to defeat humans. However, as a recent chess.com report explains, computers are now far stronger than humans:

Human chess and computer chess are different, even at the highest levels. The best humans play at an Elo rating of 2800. “Stockfish,” the most powerful chess engine, has an estimated rating of more than 3500. In a theoretical match between World Champion Magnus Carlsen vs. Stockfish, we estimate that it is most likely that Magnus Carlsen would lose every single game—no wins and no draws.

The supremacy of Machine over Man should be marked as a great triumph in artificial intelligence, and in a broad sense it is. However, I would argue that playing skill should not be the only goal, and a truly useful engine should be interpretable as well. We’ve already “solved” the problem of playing chess at an extremely high level. Yet for historical reasons, interpretability was sacrificed for the sake of speed and playing strength. However, these tradeoffs may not make as much sense today. Part 2 discusses opportunities and clear benefits for reevaluating those decisions moving forward.

Background

The general algorithm for performing search in zero-sum perfect information games like chess is known as minimax. The algorithm attempts to find the move which minimizes the opponent’s maximum (i.e. best) move. Minimax visualizes the possible future state of the game as a tree, and the value of each node in the tree as a function of the nodes following from it. If you could compute the full game tree (in simple games like tik-tac-toe this is possible), you would be able to enumerate all possible terminal nodes, and propagate the result (1 for a win, -1 for a loss, 0 for a draw) back up the tree.

That’s not possible in chess. The game tree is too big. Instead, the value of many of the nodes needs to be estimated using heuristics so that they can be propagated upwards. Therefore a fast and accurate static evaluation function is critical. (However, since the problem is recursive, the problem of creating a perfectly accurate static evaluator is as hard as evaluating that node’s entire associated game tree.)

Minimax is often augmented with “alpha-beta pruning” to reduce the number of positions which will be evaluated. This effectively cuts the computational complexity exponent in half by removing from consideration those branches which cannot affect the final result.

Other challenges in minimax evaluation exist as well. In particular, a phenomenon dubbed the “Horizon Effect” is a peculiar failure mode of minimax searches. The Horizon Effect was first described by grandmaster and computer scientist Hans Berliner in 1975. His illustration of the problem (his Figure 1.3) is reproduced in Figure 1. Algorithms that do not account for the Horizon Effect will try to “push” bad outcomes of their search beyond their search horizon, instead opting to make hopeless moves which only serve to delay the inevitable. As humans we intuitively understand this illusion.

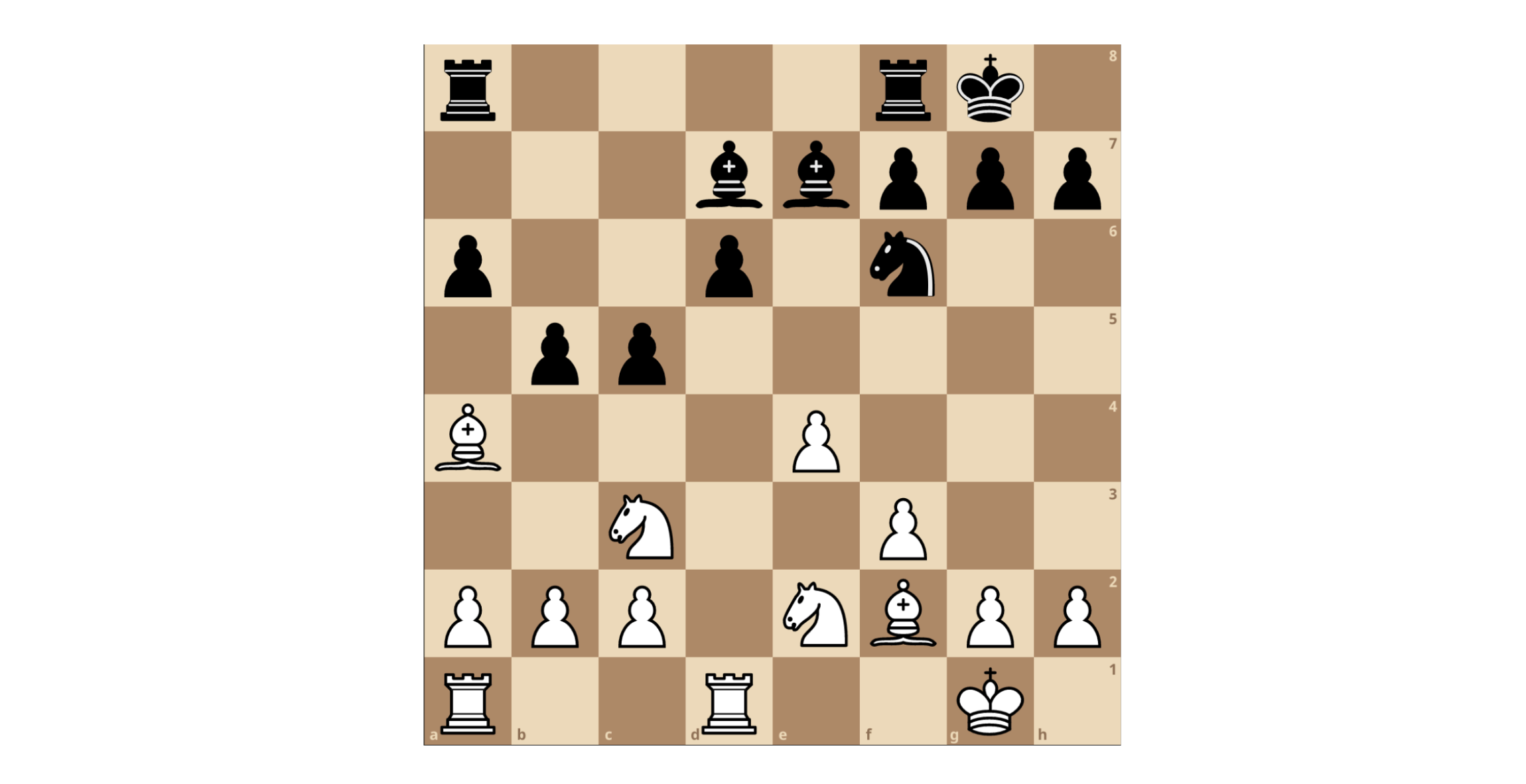
Figure 1. White to move. Here, white’s bishop on a4 is doomed, attacked by black’s pawn on b5. White could delay the inevitable by moving his bishop to b3, but then black simply seals the bishop’s fate with pawn to c4. In that position, white does not have time to save his bishop, and it will be captured no matter what on the next move by the pawn on c4. Due to the Horizon Effect, at a limited depth white will not recognize this and will play hopeless moves like pawn from e4 to e5, temporarily attacking the knight but easily parried by capturing with the pawn on d6. This phenomenon is deemed the “Horizon Effect” because by pushing negative outcomes beyond the “horizon” of calculation depth, the engine is able to trick itself into believing that the problem doesn’t exist. A true case of “see no evil”.

Figure 1. White to move. Here, white’s bishop on a4 is doomed, attacked by black’s pawn on b5. White could delay the inevitable by moving his bishop to b3, but then black simply seals the bishop’s fate with pawn to c4. In that position, white does not have time to save his bishop, and it will be captured no matter what on the next move by the pawn on c4. Due to the Horizon Effect, at a limited depth white will not recognize this and will play hopeless moves like pawn from e4 to e5, temporarily attacking the knight but easily parried by capturing with the pawn on d6. This phenomenon is deemed the “Horizon Effect” because by pushing negative outcomes beyond the “horizon” of calculation depth, the engine is able to trick itself into believing that the problem doesn’t exist. A true case of “see no evil”.

Branching Factor

In any given position, there may be many possible moves. By some estimates, chess has an average branching factor of around 30, with other estimates putting the number around 40. It isn’t easy to find a concrete value for the branching factor of chess. One source claims (without citation) that the branching factor may be up to 40 (see pg. 117). However, a more recent statistical analysis of 2.5 million chess games put the real number closer to 31.

The branching factor depends on the stage of the game; middle games have far more available moves than end games. Because not all games are the same length, shorter games will tend to have higher average branching factors than longer ones. Barnes’ graphic is reproduced above.

The branching factor depends on the stage of the game; middle games have far more available moves than end games. Because not all games are the same length, shorter games will tend to have higher average branching factors than longer ones. Barnes’ graphic is reproduced above.

In any case, it is possible to dramatically reduce the branching factor by employing “selective search”, which means excluding nodes from recursive tree search altogether. Reducing the number of possible moves that will be explored in any given position promises dramatic computational speedups, allowing the tree to be searched deeper at the expense of width. Given the slow speeds (by contemporary standards) of early computers, the allure of such a technique should be clear. It is also a more psychologically plausible way of playing, since most players quickly rule out ridiculous seeming moves and focus on the most promising ones.

Early Chess Engines

An early attempt to narrow the search tree was proposed by Berliner, who in 1975 devised CAPS-II which utilized a tree search algorithm with five total “reference levels” including ALPHA and BETA. His paper also was cognizant of the work of Chase and Simon from two years prior, recognizing the need for a bottom-up board representation. Unfortunately, his board representation was largely geometrical and included little in the way of qualitative relationships between pieces. Nevertheless, the resulting program was able to solve tactical puzzles in a quite impressive manner for the time.

Another example of the use of such a narrowed search tree is PARADISE (PAttern Recognition Applied to DIrecting SEarch). This system used a knowledge base containing 200 “production rules” to match board patterns and determine the best move at any time. An example production rule is shown in Figure 2.

Figure 2. A sample production rule from the PARADISE knowledge base. This production rule detects and acts upon opponent’s trapped pieces. A trapped piece is identified as a non-pawn defensive piece which cannot move to another square without being captured and is not already attacked. Finally, the production rule describes the threat of this action (winning the piece) and how likely it is to succeed.

Figure 2. A sample production rule from the PARADISE knowledge base. This production rule detects and acts upon opponent’s trapped pieces. A trapped piece is identified as a non-pawn defensive piece which cannot move to another square without being captured and is not already attacked. Finally, the production rule describes the threat of this action (winning the piece) and how likely it is to succeed.

Because the tree search was narrower, the system was able to search to higher depths. Still, because of hardware limitations of the time, PARADISE was extremely slow, generating only 109 nodes in 20 minutes of search time. (Current chess engines evaluate millions of nodes per second.)

PARADISE executes static analysis on a position using its many production rules with the ultimate goal of creating and executing a plan. Matched production rules post concepts to the database in addition to information about the intentions of the concept and its likelihood of success.

The program is then able to use this information to form a plan, which is a set of actions for the side to move, along with corresponding plans for each defensive alternative. Because there may be many potential alternatives at each move, this plan includes many branches.

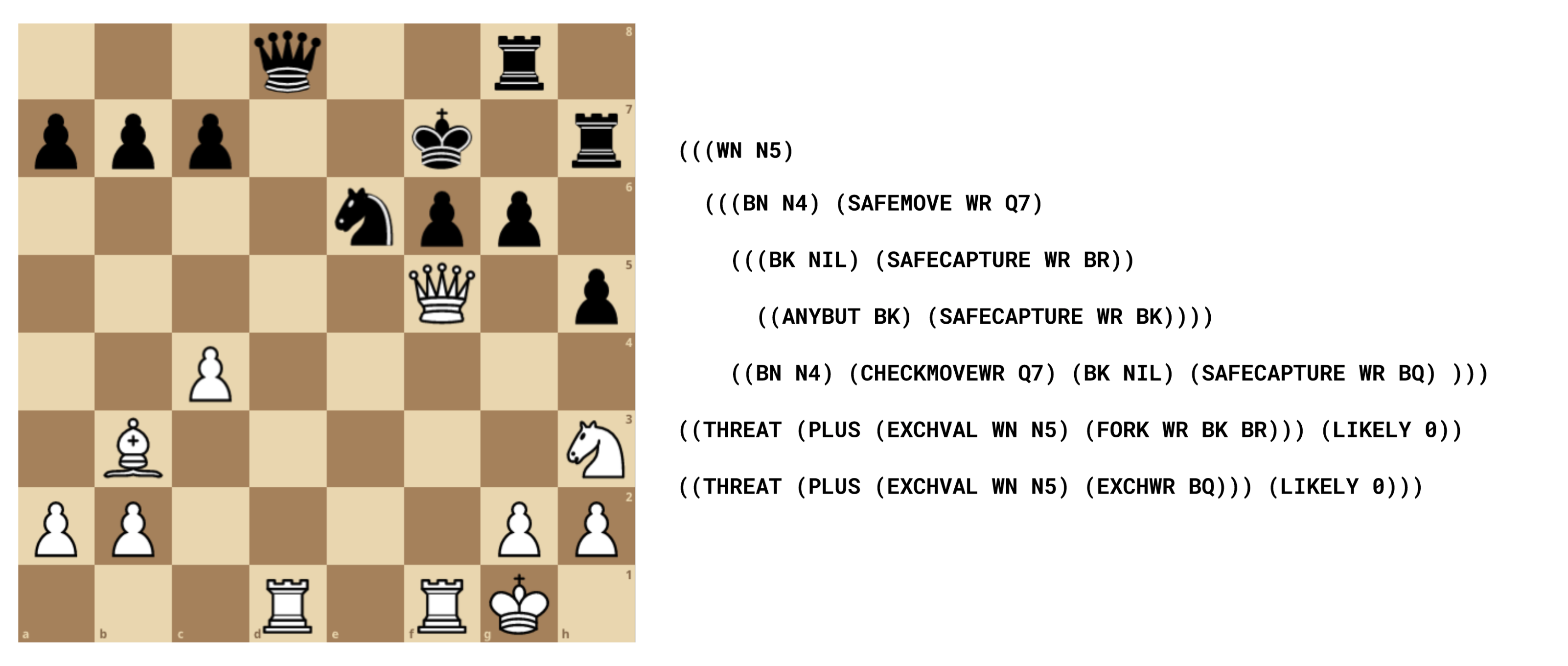
Figure 3. White to move, PARADISE has produced a plan which involves checking the black king by moving the knight to g5, then checking the black king by moving the rook to d7. Depending on black’s next move white will then try to either capture the queen on d4 or the rook on d7.

Figure 3. White to move, PARADISE has produced a plan which involves checking the black king by moving the knight to g5, then checking the black king by moving the rook to d7. Depending on black’s next move white will then try to either capture the queen on d4 or the rook on d7.

An example of such a plan is reproduced in Figure 3 above. (An interesting sidebar about this position is that based upon Stockfish analysis, this position results in inescapable checkmate for black within 15 moves. That is, even with optimal play, black will be checkmated in 15 or fewer moves. The winning sequence begins with white moving his queen to e5, exploiting the pin on the f6 pawn from the f1 rook.)

Searching only selective lines is more difficult to implement than full-width search. Further, selective searches may miss important continuations of a position, causing the computer to select an incorrect move. It was for this reason that Berliner himself, an original proponent for the application of strict logical rules in chess, decided to seek brute-force search methods instead.

Modern Chess Engines

Stockfish is currently the #1 ranked chess engine in the world. Stockfish is open-source and performs a “full width” search on the game tree. Leaf nodes are evaluated using either a classical, hand-crafted evaluation heuristic, or more recently, a neural network evaluator called NNUE. The classical evaluation function uses a set of around 30 factors weighted empirically using a dedicated testing framework called Fishtest. Altogether, the project has around 200 contributors. Optimized for speed, Stockfish can evaluate around millions of nodes per second on a typical 4-core computer.

Stockfish analyzing the starting position on my laptop at around 1 million nodes per second.

Stockfish analyzing the starting position on my laptop at around 1 million nodes per second.

Neural networks may also be used more directly. Leela Chess Zero, also known as Lc0 is another open-source chess engine, modeled after DeepMind’s AlphaZero chess engine. Lc0 uses Predictor + Upper Confidence Bound tree search (PUCT) to search its game tree. Leela evaluates new nodes by iteratively choosing moves from a probability distribution until it reaches an unexplored node. At that point, Leela’s neural network estimates the node’s value and propagates that value back up the tree. PUCT is very similar to Monte Carlo Tree Search, but with game “rollouts” replaced by neural network evaluations.

One other notable engine is Maia Chess. Maia is interesting for two reasons. Unlike most other engines, Maia’s objective is to model human behavior rather than to perform optimally. This is interesting because Maia is in many cases trained on suboptimal data. The other notable feature about Maia is the unusual manner in which moves are selected: instead of performing any type of tree search at all, the engine simply returns the neural network’s static evaluation of the current board position.

Suffice it to say, however, that despite computation no longer being a significant limitation, prior qualitative approaches still have garnered relatively little attention.

Conclusion

Engineers have historically sought to build the most powerful chess engine possible. With the singular goal of defeating human (and now computer) opponents, explainability was an expedient but understandable tradeoff to make. In the present day, however, there is no longer a question of whether humans or computers are superior chess players. It seems quite clear that the time has come to revisit some of the tradeoffs made in the past.

In part 2 I will discuss some clear benefits of a more interpretable chess engine, and some possible routes of getting there.