4 minutes
Paper Summary: Dual-Encoders in Ranking
In Defense of Dual-Encoders for Neural Ranking by Menon et. al. discusses the question of why dual-encoder (DE) models, also called Bi-Encoders elsewhere, don’t match the performance of cross-attention (CA) models. The authors investigate what is actually going on, and demonstrate some improved performance over baseline DE models with a new model distillation method.
Background
Search requires an automatic way to find the most relevant documents to a query. There are bag-of-word approaches to this task (for example BM25) and neural approaches. An example of a bag-of-words approach might simply be to count the number of similar words between the query and each document, and return the document with the highest number of similar words. There are word-stuffing issues with this idea, but the larger issue is that a bag-of-words strategy can’t account for synonyms. If I search for bad guy I will never find villain without some additional logic to account for this. A neural network implicitly understands the relationship between words, and avoids the fragile logic of simple word counts.
The idea of a neural encoding approach is pretty simple. For each document in your corpus, pass the query a document into a function which will return a similarity score between 0 and 1. Then, just sort the documents by that score. There are two main architectures for doing this: dual-encoders and cross-attention models.
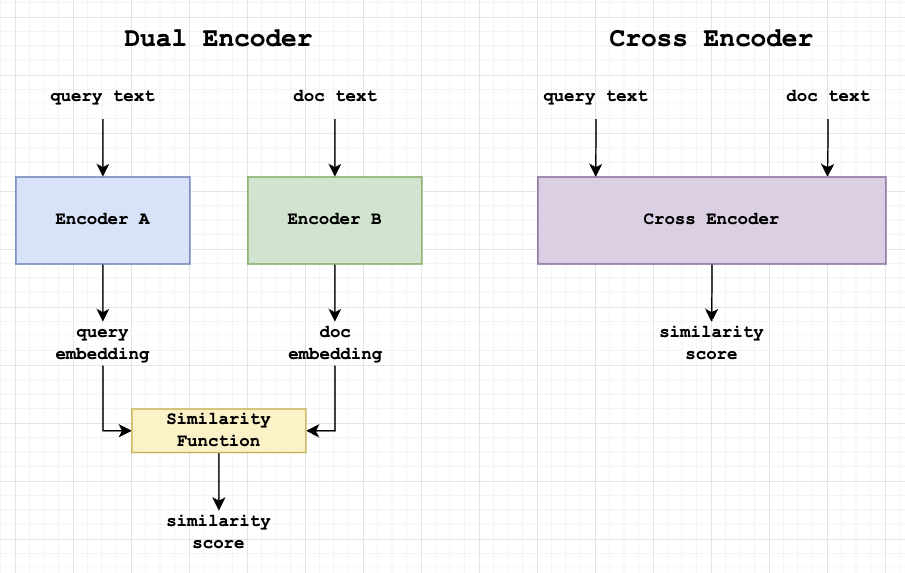
Dual encoder architectures can precompute document embeddings but tend to be less accurate than cross attention models.
The great thing about DE models is that document embeddings can be computed ahead of time. When users enter a query, only that query embedding needs to be calculated, and then compared with the embeddings already calculated for each of the documents. It’s a lot faster. So much faster, in fact, that CA is generally not used for initial retrieval, only for reranking afterwards.
However, DE models tend to be less accurate than CA models. It would be great if it was possible to transfer some of the benefits of CA models to DE models.
The Problem
It’s unclear whether the shortcomings of DEs are due to the DE model’s capacity or because of its training procedure. DEs may be overfitting.
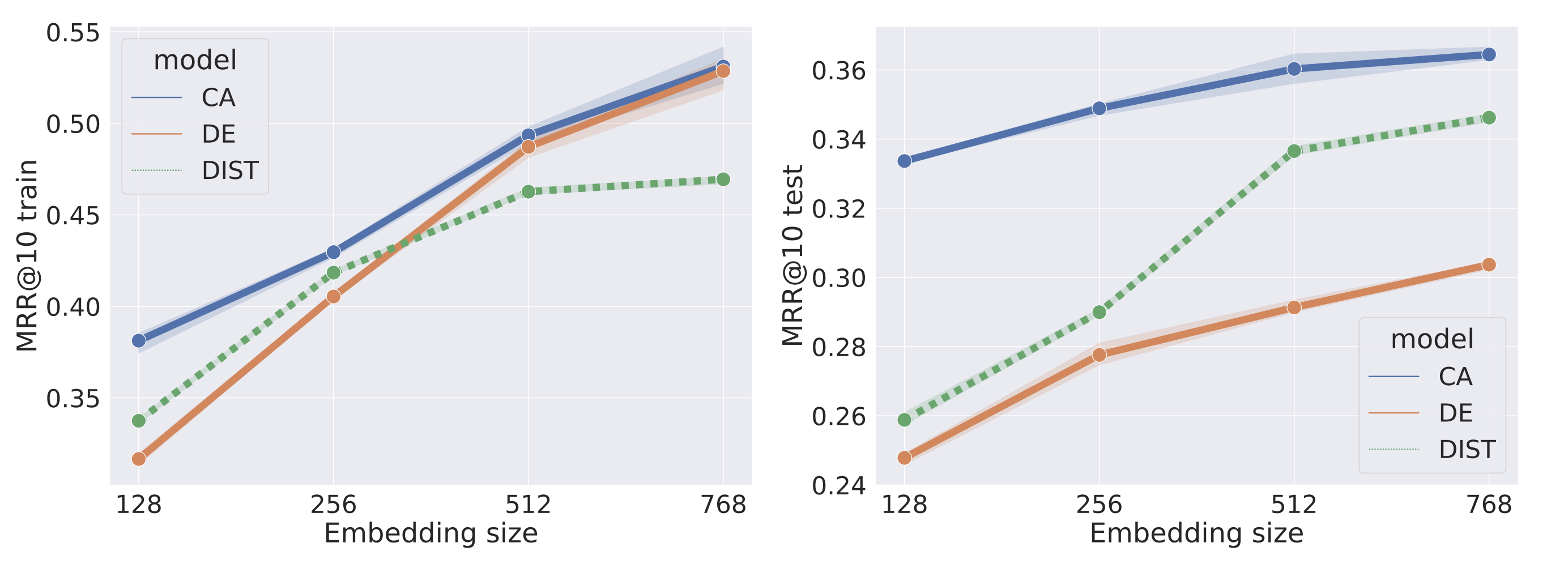
DE models can match CA model training performance but are often lower during evaluation.
Dual encoders can also be improved by distillation, of which there are two kinds:
- Logit matching. Try to match embeddings between teacher and student.
- Probability matching. Try to match the softmax probabilities between teacher and student.
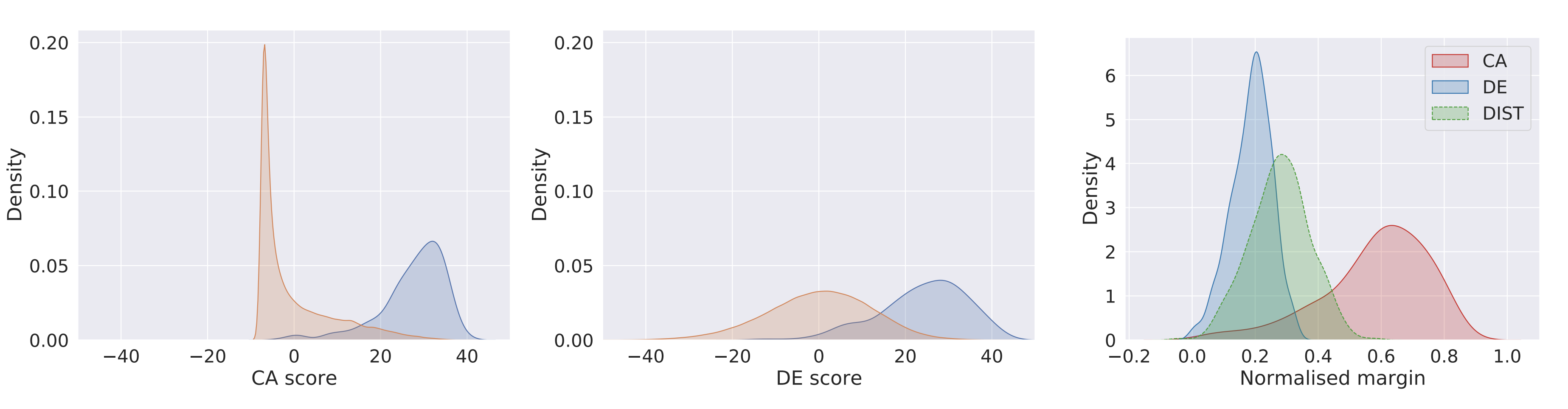
CA models have better separation between positive and negative examples, strongly predicting negative examples. DE models have more overlap between positive and negative predictions. Normalizing the margins between positive and negative predictions (higher is better), CA models clearly have better performance. The distilled model is slightly better than the DE model.
Part of the cause of this discrepancy may be the fact that DE models have noisier updates. DE models may have difficulty modeling negative scores since updating their weights on positive (q, d+) pairs can inadvertently increase scores for negative (q, d-) pairs. Dropout also doesn’t seem to mitigate overfitting.
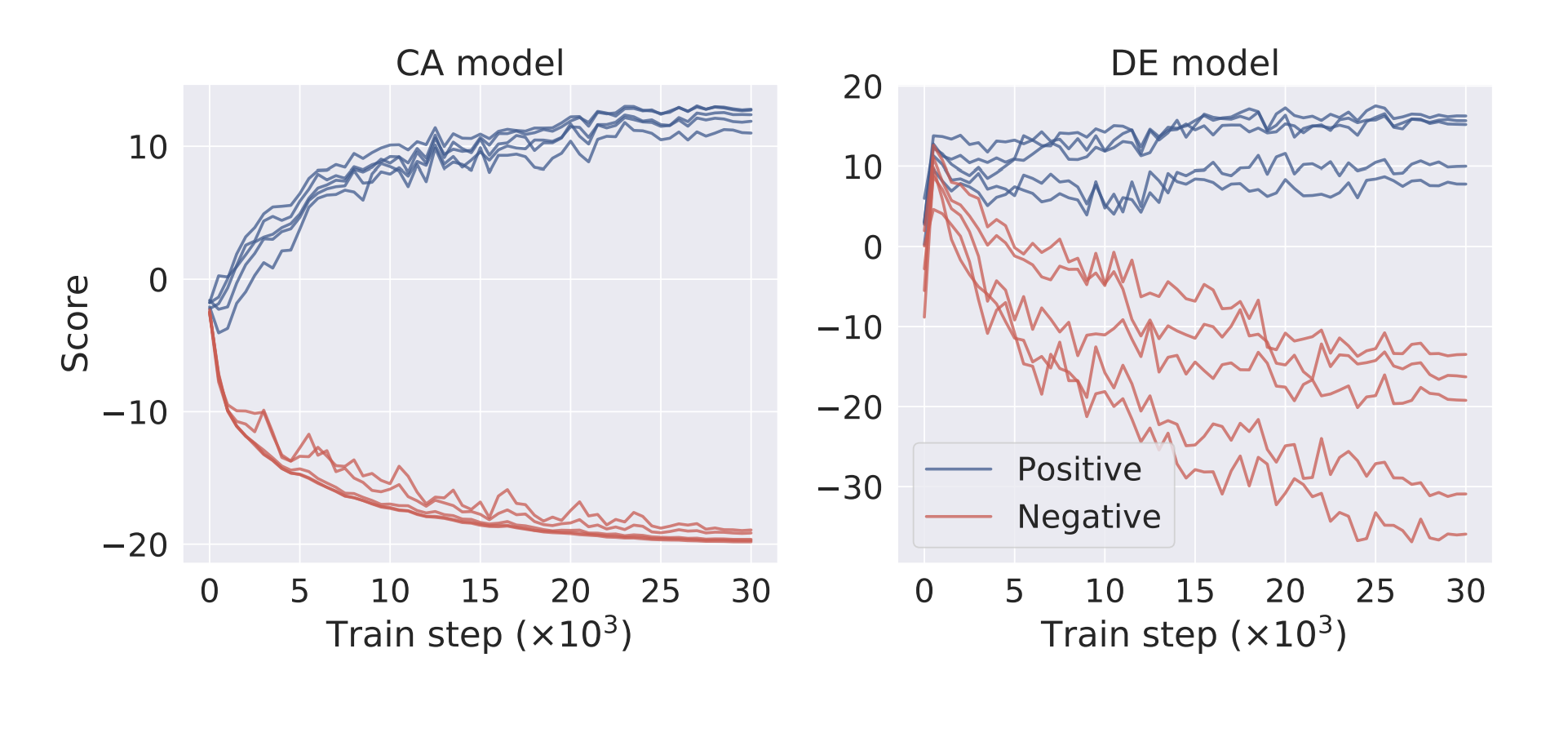
The evolution of scores for five positive and five negative documents for a fixed query. Scores from the CA model separate much more smoothly than in the DE model.
Solutions
Previous work has tried to improve training procedures in several ways:
- Adjusting the scoring layer. Usually embeddings are scored with a simple dot product, but a more sophisticated scoring function may be able to capture more information at the cost of inference speed.
- Distilling predictions from CA models. Model distillation uses a teacher-student framework where the smaller “student” model attempts to mirror the “teacher”. This paper explores a new approach to distillation.
The authors introduce multi-margin MSE loss (M3SE):
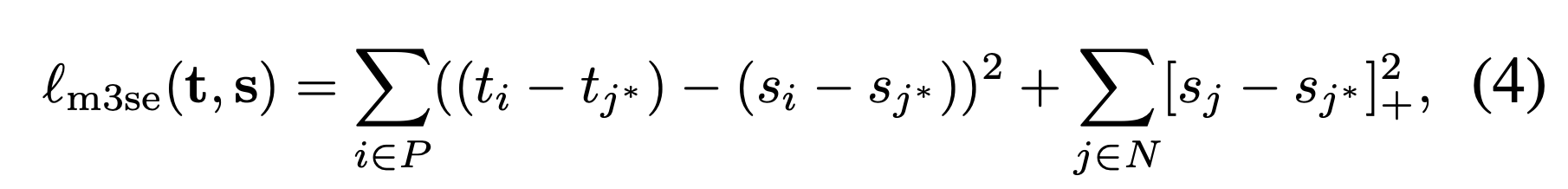
M3SE loss attempts to match the margins of score differences between teacher and student. For performance reasons, however, rather than matching each margin, it only encourages the student to be less than or equal to the teacher’s highest negative score.
M3SE can be seen as an extension of Margin MSE loss where instead of matching logits it matches raw scores. It can also be seen as a smooth approximation of softmax cross-entropy loss. The authors also highlight parallels between M3SE and RankDistil.
Results
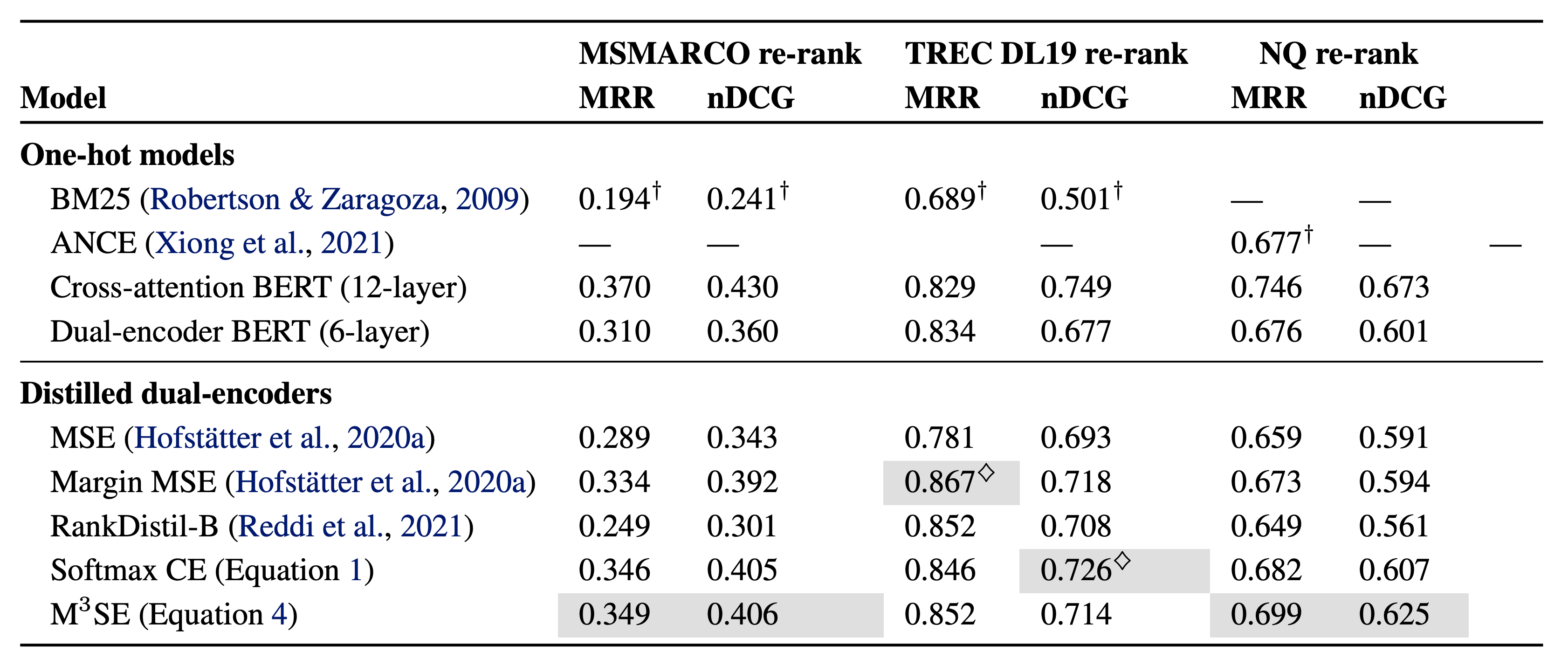
Apart from TREC, M3SE distillation appears to nearly close the gap with cross-attention models. Distilled models are 6-layer BERT models with embedding size 768.